# 위상정렬
위상정렬은 사이클이 없고 방향은 있는 비순환 방향 그래프(DAG : Directed Acyclic Graph)를 순서대로 출력하는 알고리즘 입니다.

그림에서 E노드는 C와 F노드 모두에 의존성이 있어서 C,F노드 모두 방문하고 E노드가 방문되어야 합니다.
그래프의 방문결과가 순서대로 출력되어야 하기 때문에 그래프의 시작점과 방향이 존재해야하는데, 만약 사이클이 있으면 위상정렬로 정렬할 수 없습니다.
리스트같은 경우는 그 자체로 순서가 있지만, 그래프와 같이 비선형적이지만 순서가 있는 작업의 경우 그 순서를 찾아주는 알고리즘으로 위상정렬을 사용합니다
위상정렬은 O(|V| + |E|)의 시간복잡도를 가지는데, 그래프에 존재하는 버텍스의 수와 엣지의 수와 비례하기 때문에 비교적 빠른 수행이 가능하다는 특징이 있습니다
# 구현 방법
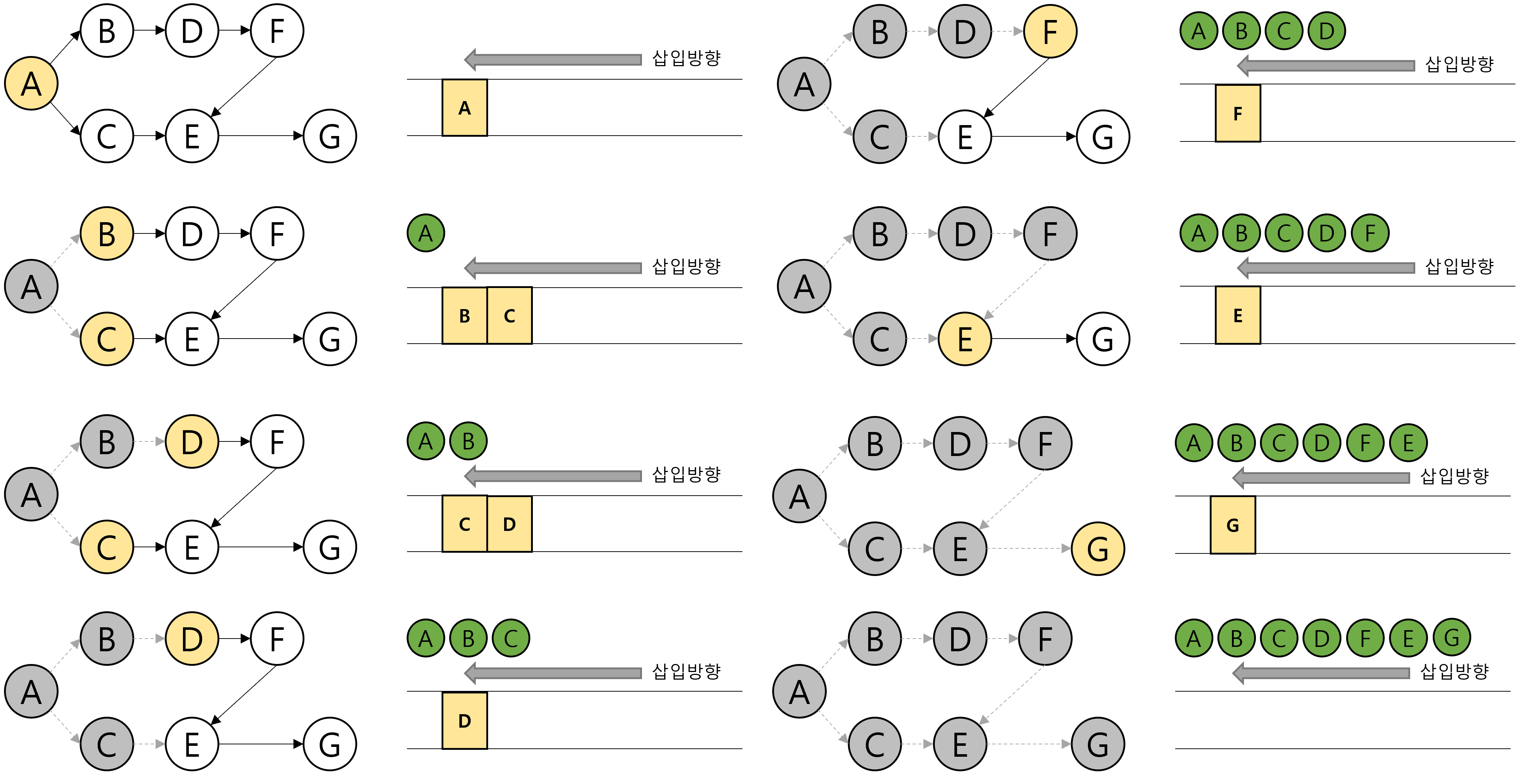
[ queue로 구현하는 방법 ]
큐는 진입차수를 계산하면서 사용하게 되는데, 진입차수(indegree)는 한 노드에 들어오는 다른 간선의 수를 의미합니다. 동작 방법은 아래와 같습니다.
1. 모든 버텍스의 indegree 수를 센다
2. 큐에 indegree가 0인 노드 삽입
3. 큐에서 노드를 꺼내 연결된(나가는방향 outdegree) edge 제거
4. 3번으로 인해 ingderee가 0이된 노드를 큐에 삽입
5. 큐가 빌 떄 까지 반복
*주의!*

(왼쪽 그래프) 진입차수가 0인 A노드부터 시작하게 됩니다. 사이클이 있는 경우 그 노드는 항상 진입차수가 1이상이기 떄문에, 큐에 들어가지 못합니다.
(오른쪽 그래프) 집입차수가 0인 노드가 없는 경우에는, 아예 위상정렬을 시작할 수 없습니다
[ stack으로 구현하는 방법 ]
스택으로 구현하는 방법은 DFS의 역순으로 동작한 결과가 위상정렬이 된다고 생각하면 됩니다. DFS는 깊이우선탐색으로 최대한 멀리들어가야한다 했습니다.

동일하게 A노드부터 시작해서 들어가게 되는데, DFS로 A와 연결된 노드 B,C를 순서대로 방문하게 되면 먼저 B노드를 타고 들어가서 B,D,F,C,G노드로 DFS 방문을 하게 됩니다. 그리고 DFS 역순인 G,E,F,D,B노드를 스택에 삽입해줍니다. 스택은 FIFO 구조이므로 B노드가 스택의 가장 위에, G는 가장 아래에 위치하게 됩니다.
** 이때, A노드는 아직 방문하지 않은 상태입니다. 왜냐하면 아직 연결된 노드(C노드)를 다 탐색하지 않았기 떄문입니다.

그 다음. A에 연결된 C노드를 방문하고, 스택에 쌓아줍니다 (연결된 E,G노드는 이미 스택에 쌓여있습니다)

마지막으로 A노드를 스택에 쌓아줍니다. 더 이상 DFS탐색을 할 노드들이 존재하지 않는다면 스택에 있는 노드들을 차례로 출력해주고, 이 결과 A-C-B-D-F-E-G가 위상정렬의 결과가 됩니다
'Computer Science > Data Structure' 카테고리의 다른 글
| BFS, DFS (0) | 2022.08.26 |
|---|---|
| Graph (0) | 2022.08.25 |
| Heap (0) | 2022.08.23 |
| Binary Search Tree (BST) (0) | 2022.08.22 |
| Binary Tree (0) | 2022.08.21 |