# Binary Tree
이진트리는 각 노드가 최대 2개의 자식 노드를 가지는 트리입니다. 최대 2개 이기 때문에 자식노드가 없을 수도 있고, 하나만 있을 수도 있습니다. 이 때, 자식노드는 각각 왼쪽 자식노드와 오른쪽 자식노드로 표현합니다. 그래서 같은 루트에 같은 자식 루트를 가지고 있어도 자식노드가 왼쪽이냐 오른쪽이냐에 따라 두 트리는 서로 다른 트리가 됩니다.
[ 정 이진트리 : Full Binary Tree ]

모든 노드가 2개의 자식을 가지거나 자식이 없는 트리를 정 이진트리(full binary tree) 혹은 엄격한(strict) 이진트리라고 합니다.
[ 포화 이진트리 : Perfect Binary Tree ]

모든 노드가 2개의 자식을 가지고 leaf 노드가 같은 레벨인 트리를 포화이진트리(perfect binary tree)라고 합니다. 포화이진트리는 높이가 h일 때, 노드의 갯수는 (2^(h+1) -1)개이며, leaf노드의 갯수는 (2^h)개 입니다.
[ 완전 이진트리 : Complete Binary Tree ]

마지막 레벨을 제외하고 모든 노드가 채워진 트리를 완전 이진트리(complete binary tree)라고 합니다. 완전 이진트리에서 노드는 왼쪽에서 오른쪽으로 채워집니다. 만약 오른쪽 노드가 채워져있다면 완전 이진트리에서는 왼쪽 노드도 무조건 채워져 있어야 합니다.
포화이진트리는 완전 이진트리의 조건을 충족하기 때문에 완전이진트리라고 할 수 있습니다 (하지만, 역은 성립되지 않습니다)
# 이진트리의 일차원 배열
이진트리는 선형구조인 일차원 배열로 표현가능하다는 특징을 가지고 있습니다,
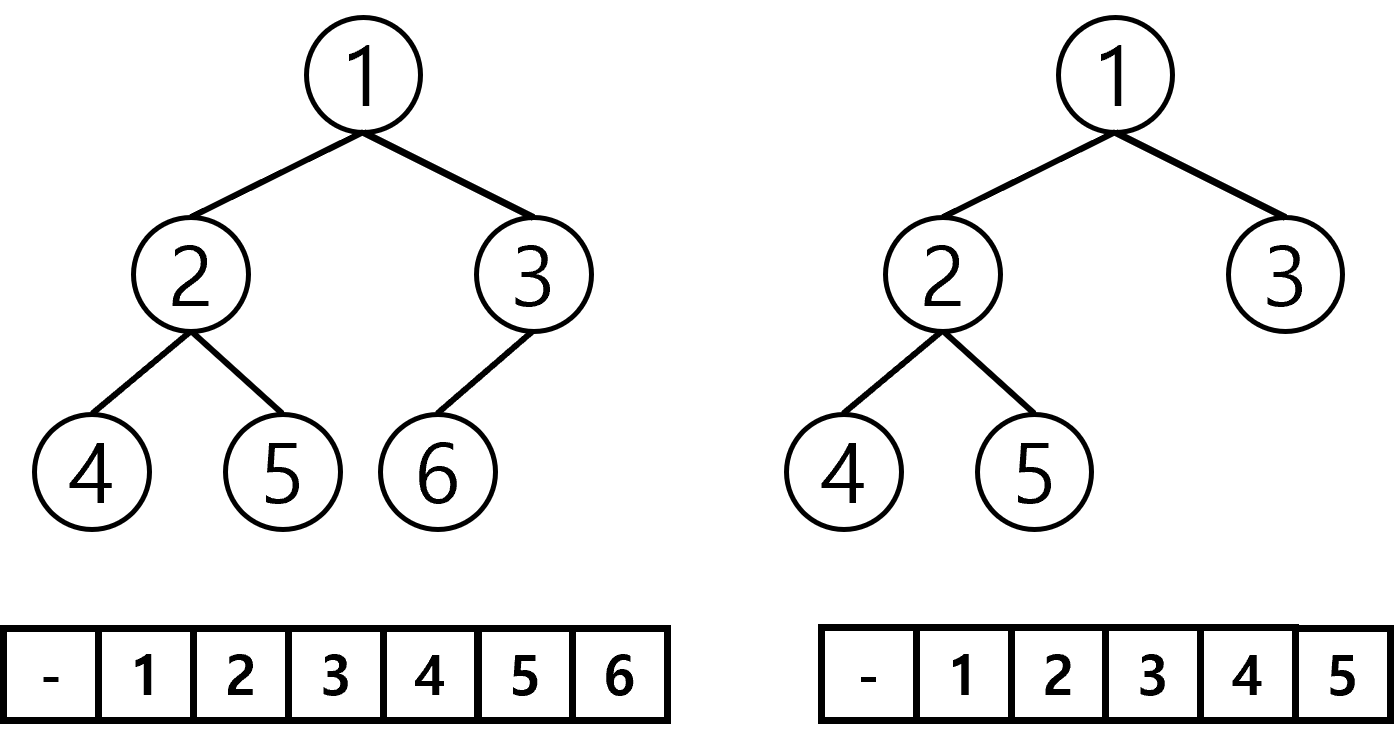
루트에서부터 왼쪽노드에서 오른쪽노드로 순서를 매기는데, 완전 이진트리 같은 경우에는 빈자리가 없기 때문에 각 번호르 인덱스로 써서 일차원배열로 표현 가능합니다 (완전 이진트리는 일차원 배열에서 빈틈없이 값을 채울 수 있습니다)

중간에 빈 값이 있는 이진트리는 배열로 표현하면 빈자리에 null값이 들어간 일차원배열로 표현할 수 있습니다
이렇게 일차원 배열로 트리를 표현할때는 0번째 인덱스를 비워두고 1번째 자리부터 root값을 넣습니다. 이렇게 하면 아래의 표와 같이 인덱스 위치로 찾을 수 있는 몇 가지 연산이 있기 때문입니다.
| node | index |
| 루트노드 | 1 |
| 노드i의 부모 | i / 2 |
| 노드i의 왼쪽자식 | i * 2 |
| 노드i의 오른쪽자식 | ( i * 2 ) + 1 |
일차원배열로 이진트리를 표현하면 간단하게 트리를 표현할 수 있다는 장점이 있지만, 배열의 한계(공간의 제약, 데이터 삽입삭제에 있어 기존데이터들의 이동)의 단점은 여전히 극복할 수 없기 때문에 노드의 연결로 트리를 표현하게 됩니다.
# 트리 순회
트리 구조에서 각 노드를 한번씩 방문하는 과정을 트리 순회라고 합니다. 트리를 탐색하는 방법에는 전위탐색, 중위 탐색, 후위탐색이 있습니다.
[ 전위 탐색 : preorder ]
전위탐색은 노드방문 → 왼쪽 서브트리 탐색 → 오른쪽 서브트리 탐색 순 여기서 서브트리를 preorder한다는 것은 재귀호출로 탐색이 이루어진다는 것을 의미합니다. 트리의 특성에서 말한바와 같이 트리의 하위노드는 서브트리를 구성하는 재귀적 형태이기 때문에 재귀 호출로 탐색이 가능합니다. (탐색 방식과 상관없이 무조건 루트노드부터 시작)
경로 : A – B – D – H – E – C – F – I – J – G – K

[ 중위 탐색 : inorder ]
중위 탐색은 왼쪽 서브트리 탐색 → 노드방문 → 오른쪽 서브트리 탐색 순으로 이루어집니다.
경로 : D - H - B - E - A - I - F - J - C - G - K

[ 후위 탐색 : postorder ]
후위 탐색은 왼쪽 서브트리 탐색 → 오른쪽 서브트리 탐색 → 노드방문 순으로 이루어집니다.
경로 : H - D - E - B - I - J - F - K - G - C - A

..
'Computer Science > Data Structure' 카테고리의 다른 글
| Heap (0) | 2022.08.23 |
|---|---|
| Binary Search Tree (BST) (0) | 2022.08.22 |
| Tree (0) | 2022.08.18 |
| Quick Sort (0) | 2022.08.18 |
| Merge Sort (0) | 2022.08.18 |