규제화란?
임의로 모델의 복잡도를 제한하는 방법으로, overfitting(과적합) 문제를 해결하는 방법 중 하나입니다. 테스트 시에 발생하는 에러(과적합)를 줄이기 위해, 가중치에 패널티를 부과하여 비용함수를 키워 과적합을 줄입니다

- J(w) : 목적함수(손실함수)
- Ω(w) : 규제화함수 , 학습하는 반경(범위)를 조절
- λ : 규제의 강도를 조절하는 파라미터로 0.01~0.00001 정도 값을 사용함
규제화 함수 중 가장 쉽게 더할 수 있는 것 중 하나는 weight의 norm을 구하는 것입니다.
Norm?
벡터의 크기(혹은 길이)를 측정하는 방법이며, 두 벡터사이의 거리를 측정할 수 있습니다


규제화함수 Norm 종류
L1 regularization (Lasso)

- n=1인 norm입니다.
- 가중치의 절댓갑 합을 손실함수에 더합니다.
- L1을 사용한 손실함수 : (wx+b-y)^2+λ|w|
- |w1|+|w2|+...+|wd| → v자형 벡터를 가짐
- 최소 제곱 오차의 함수 등고선과 규제 영역의 교점에서 최적의 값이 생깁니다
- 각 방법에 대해 가능성을 유지하면서 손실함수를 최소화하는 것이 목표이므로 등고선과 규제 영역의 교차점을 찾아야 합니다.
- 지나치게 bias를 낮추는 것을 방지해서 결과적으로 overfitting을 막을 수 있습니다.
- L1의 교점은 규제 영역 모서리 맨끝에서 생길 경우가 많은데 이때, w=0이 되어 sparsity가 생긴다는 장점이 있습니다.
- 많은 파라미터들이 0이 되기 때문에, 파라미터가 줄어들어 모델이 압축이 되는데 이때 컴퓨팅 코스트를 줄일 수 있습니다.
- w가 0이 되는 feature는 거의 쓰지 않는 특성이라 판단합니다 (= feature selection, 특성선택의 효과)
- 0이 아닌 특성을 주로 볼 수 있기 때문에 모델이 더 나은 해석능력을 가질 수 있습니다
- L1을 미분할 경우 유일한 해가 아닐 수 있습니다 (solution이 불안정함)
- L1을 SGD로 구할 경우, sparse하게 하는 solution이 아닐수 있습니다
- SGD는 최적해를 한번에 구하는 것이 아닌, 점차 근사해나가는 방법이기 때문입니다
tensorflow.keras.regularizers.l1(l=0.01)
L2 regularization (Ridge)
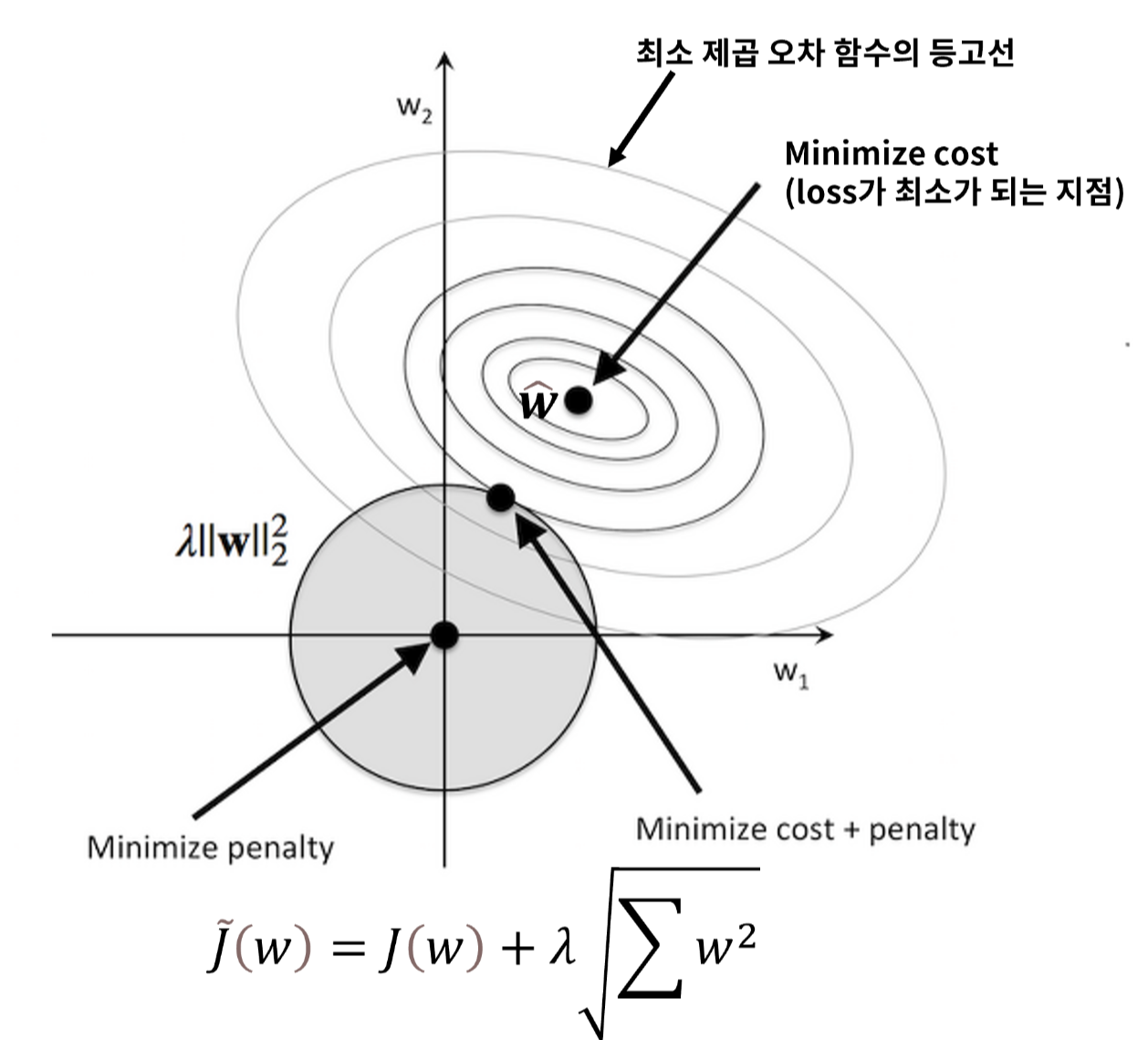
- n=2인 norm입니다.
- 가중치의 제곱합을 손실함수에 더합니다.
- L2을 사용한 손실함수 : (wx+b-y)^2+λ(w^2)
- 최소 제곱 오차의 함수 등고선과 규제 영역의 교점에서 최적의 값이 생깁니다
- 각 방법에 대해 가능성을 유지하면서 손실함수를 최소화하는 것이 목표이므로 등고선과 규제 영역의 교차점을 찾아야 합니다.
- 지나치게 bias를 낮추는 것을 방지해서 결과적으로 overfitting을 막을 수 있습니다.
- 원과 같은 형태이므로 교점이 원이 접하는 어디든 균등하게 될 수 있습니다.
- w가 0이 되는 경우가 L1에 비해 적습니다

- L2를 미분하면 λw가 되는데, 이것이 w업데이트 양(-)에 추가되어 결국 자기 자신의 크기에 비례하는 속도로 감소합니다 (=가중치감쇠, weight decay)
tensorflow.keras.regularizers.l2(l=0.01)

| L1 | L2 | |
| outlier에 강한가? | O | X (제곱을 취하기 때문) |
| Stable한가? | X | O |
| 유일해를 같는가? | X | O |
| feature selection효과? | O | X |
| sparsity? | O | X |
'AI > Deep Learning' 카테고리의 다른 글
| Dropout (드롭아웃) (0) | 2022.11.11 |
|---|---|
| Data Augmentation (데이터 증식) (0) | 2022.11.07 |
| CNN (Convolution Neural Network, 합성곱 신경망) (0) | 2022.11.03 |
| Batch Normalization (배치정규화) (0) | 2022.10.22 |
| loss function (손실함수) (0) | 2022.10.20 |