Support Vector Machine (SVM, 서포트백터머신)

SVM이란?

서포트백터머신은 매우 강력한 다목적 머신러닝 모델이자 가장 있기 있는 모델입니다. 선형분류, 비섢형 분류, 회귀, 이상치 탐색에 활용되며, 복잡한 분류 문제에 잘 맞고 작거나 중간크기 데이터셋에 적합합니다.

• 패턴 인식, 자료 분석을 위한 지도 학습 모델
• 주로 분류와 회귀 분석을 위해 사용
• 두 카테고리 중 어느 하나에 속한 데이터릐 집합이 주어졌을 떄, 새로운 데이터가 어느 카테고리에 속할지 판단하는 '비확률적' 이진 선형 분류 모델
• 사상된 공간에서 경계로 표현되는데, 그 중 가장 큰 폭을 가진 경계를 찾는 알고리즘

 

선형 SVM 분류

SVM분류기(Large Margin Classification,라지 마진 분류)는 클래스 사이에 폭이 가장 넓은 결정 경계를 찾아내는 것입니다.

• Margin : 두 데이터 군과 결정경계가 떨어져있는 정도

• 위 그림에서 경계 바깥쪽에 훈련 샘플은 추가하는 것은 마진에 영향을 미치지 않습니다
• 서포트벡터란? 두 클래스 사이의 경계에 위치한 데이터 포인트들을 의미하며 결정 경계를 만드는 데 영향을 미치기 때문에 서포트벡터라고 합니다.
• 즉 결정 경계는 경계에 위치한 샘플인 서프트 백터에 의해 결정됩니다

• SVM 분류모형은 변수 스케일이 중요한데, 결정경계를 더 정확하게 설정할 수 있기 떄문입니다.

[ 하드 마진 분류 ]

모든 샘플이 결정 경계 바깥쪽에 올바르게 분류 되어있는 모형입니다.

[ 소프트 마진 분류 ]

선형적으로 구분이 어려운 샘플이 존재할 때, 결정경계의 폭을 가능한 넓게 유지하면서, 적절히 분류 모형 성능(마진 오류를 줄일 수 있도록)을 고려한 모형입니다.

[ SVM의 하이퍼파라미터 'C' ]

• C값을 높게 설정하면 마진 오류가 줄어들지만, 결정 경계가 좁아집니다
• C값을 낮게 설정하면 마진 오류가 커지지만, 결정 경계가 넓어집니다
• 즉, 과대적합을 줄이고 싶으면 C값을 줄이는 방식으로 규제가 가능합니다.

 

비선형 SVM

선형 SVM 분류기가 효율적이고 많은 경우에 잘 작동하지만 선형적으로 분류할 수 없는 데이터셋 또한 굉장히 많은데, 이 데이터셋에 대해 비선형성을 기반으로 차원을 변환시켜주면 서포트벡터로 분류할 수 있기 때문에 비선형 SVM이 필요합니다.

polynomial_svm_clf = Pipeline([
        ("poly_features", PolynomialFeatures(degree=3)),
        ("scaler", StandardScaler()),
        ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
    ])

위의 코드와 같이, PolynomialFeatures를 활용해 차원을 높혀줄 수 있습니다. 

• 하지만, Polynomial 특성 추가 방법론은 낮은 차수의 다항식은 과소적합을 발생시키고, 높은 차수의 다항식은 과대적합을 발생시키는 문제점이 존재합니다.

[ 커널 트릭 ]

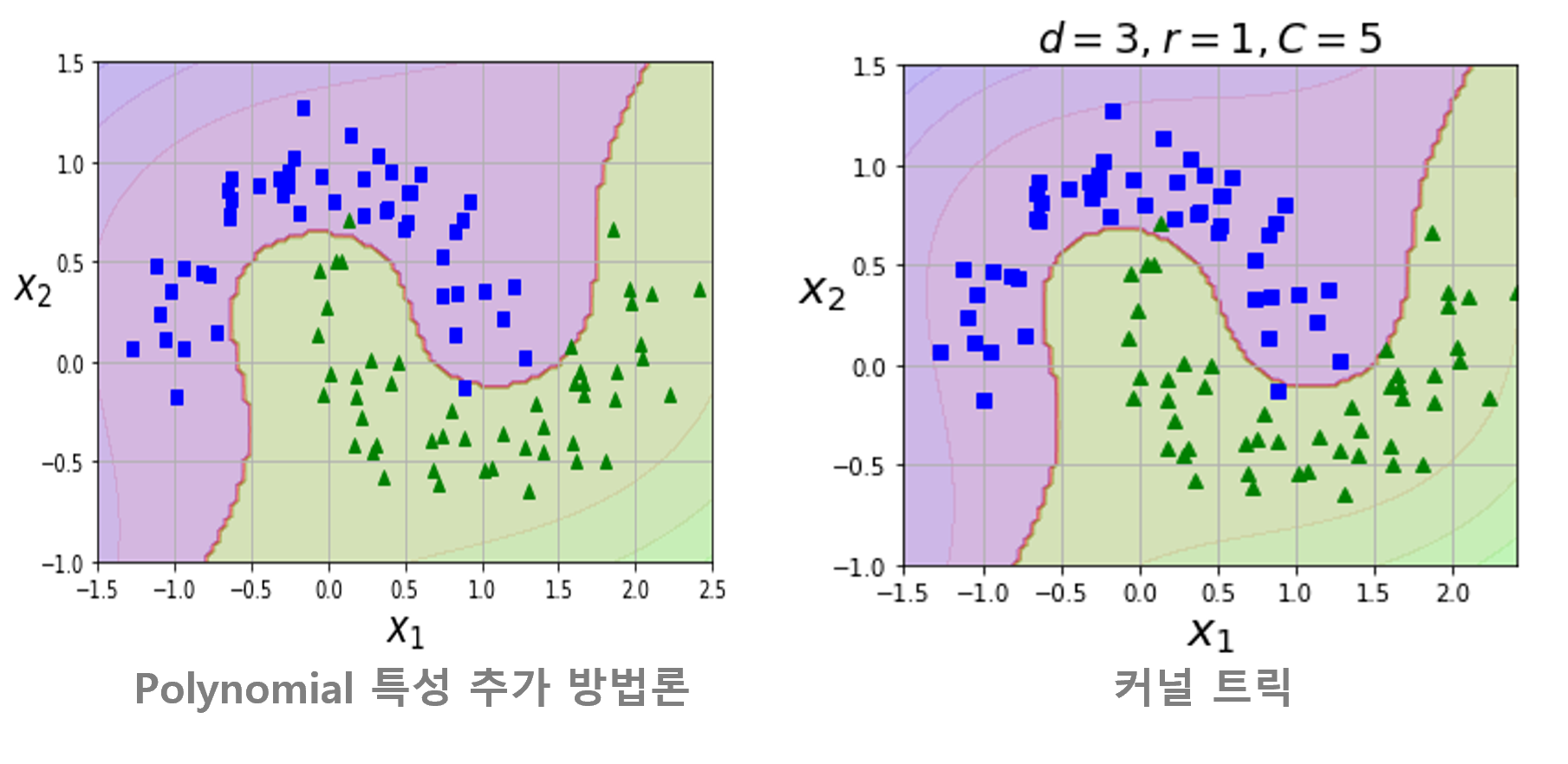
• Polynomial 특성 추가 방법론의 문제점을 커널 트릭을 통해 보완할 수 있습니다
• 다항식 커널 활용시, 실제로는 특성을 추가하지 않으면서 다항식 특성을 많이 추가한 것과 동일한 결과를 얻을 수 있습니다
• 실제로 어떠한 특성도 추가하지 않아 수많은 특성 조합을 생성하지 않으므로 모델이 느려지는 것을 방지할 수 있습니다.

poly_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
    ])

 

 

[ 유사도 특성 ]

• 유사도 특성이란? 커널 기법을 통해 유사한 분포를 가지는 변형된 변수(특성)
  • 커널 기법이란? 비선형 분류를 하기위해서 주어진 데이터를 고차원 특징 공간으로 확장 시키는 작업
• RBF kernel : 비선형으로 SVM을 학습하는데 중요한 기준이 됩니다
  • 2차원의 데이터를 kernel 이라는 단계로 올려서(차원을 높혀서) 그 차원안에서 마진을 위한 경계를 설계
  • 대표적인 유사도 함수 중, 가장 많이 사용되는 것은 가우시안 방사 기저 함수(RBF)입니다.

rbf_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
    ])

• gamma는 증가시키면, 더 좁은 종모양으로 변환됩니다
• C를 증가시키면 오차는 줄지만, 결정경계가 좁아집니다.
  • 결정경계가 좁아진다 = 좀 더 많은 특성들을 과대적합해서 예측시킨다

 

SVM 분류 방법론 정리

• 시간 복잡도에서 m은 데이터 갯수, n은 변수의 갯수
• SVC는 비선형 SVM인 경우, 커널에 따라 학습에 굉장히 오랜 시간이 소요될 수 있습니다.

[ SVM 분류 모형 훈련시 TIP ]

• 모델의 복잡ㄷ도를 조절하려면, gamma와 C를 함께 조정해주는 것이 좋다.
• 여러가지 커널 중, 가장 먼저 선형 커널을 시도해보는 것이 좋다
  • 속도 체크와 기초 성능 수준 확인 측면에서 선형커널이 다른 커널에 비해 매우빠름
  • 특히 훈련 세트가 매우 크거나 특성 수가 많은 때는 더욱 중요함
• 훈련 데이터 갯수와 변수 개수가 많지 않다면, 가우시안 RBF 커널을 이용하면 높은 성능을 기대할 수 있다 

 

SVM 회귀

SVM 회귀는 일정한 마진 오류 안에서 두 클래스 간의 결정경계 폭이 가능한 최대가 되도록하는 것은 SVM 분류와 동일하지만, 다음과 같은 차이점이 있습니다.

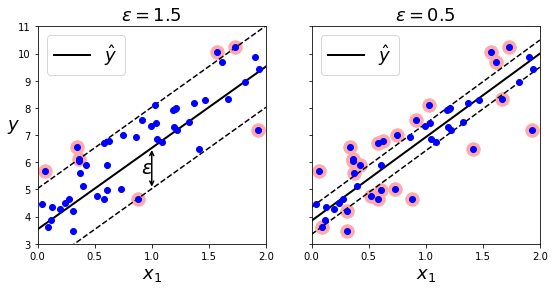
• SVM 회귀는 제한된 마진 오류(경계 밖의 샘플)안에서 경계 안에 가능한 많은 샘플이 들어가도록 학습합니다
  • 경계 폭은 ε으로 조절합니다
• 따라서, SVM을 분류가 아닌 회귀에 적용하려면 목표를 반대로 설정해야 합니다.
  • 분류 : 경계 바깥에 데이터가 최대한 많도록
  • 회귀 : 경계 안에 데이터가 최대한 많도록

svm_reg = LinearSVR(epsilon=1.5, random_state=42)

• tolerance(허용오차)와 epsilon(경계의 폭)은 다른 것
• 마진 안에서 훈련 샘플이 추가되어도 모델의 훈련 및 예측에 영향을 주지 않습니다
  • epsilon에 민감하지 않음

 

비선형 SVM 회귀

svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")

• C를 조절해 회귀모형을 규제할 수 있습니다
• 사진의 왼쪽의 그래프는 규제가 거의 없는 경우(큰 C), 오른쪽 그래프는 규제가 많은 경우입니다(작은 C)

 

 

# 코드 참고

GitHub - sonzwon/TIL_DL