Ensemble (앙상블)
앙상블이란?
앙상블은 여러 개의 분류기를 생성하고, 그 예측을 결합함으로써 보다 정확한 최종 예측을 도출하는 방법입니다.
- 앙상블은 각 분류기가 약한 학습기일지라도, 충분하게 많고 다양하다면 앙상블 모형은 강한 학습기가 될 수 있습니다.
- 앙상블은 모든 분류기가 완변하게 독립적이고, 오차에 상관관계가 없어야 최고 성능을 발휘합니다. 그래서 다양한 다양한 분류기를 얻기 위해서는 각기 다른 알고리즘으로 학습시켜야 합니다.
앙상블의 종류
◆ Voting
여러 종류의 알고리즘을 사용한 각각의 예측 결과에 대해 투표를 통해 최종 결과를 예측하는 방법입니다.
① Hard voting, 직접 투표
다수결의 원칙과 비슷한 방법으로 투표해서 최종 결과 예측

# hard voting
log_clf = LogisticRegression(solver='lbfgs', random_state=42)
rnd_clf = RandomForestClassifier(n_estimators=100, random_state=42)
svm_clf = SVC(gamma='scale', random_state=42)
voting_clf = VotingClassifier(
estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
voting='hard'
)
voting_clf.fit(X_train, y_train)
for clf in (log_clf, rnd_clf, svm_clf, voting_clf):
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print(clf.__class__.__name__, accuracy_score(y_test, y_pred))
"""
LogisticRegression 0.864
RandomForestClassifier 0.896
SVC 0.896
VotingClassifier 0.912
"""② Soft voting, 간접 투표
각 알고리즘 기반으로 예측된 레이블 값 결정 확률들을 평균 내서 가장 높은 확률의 레이블값을 최종 값으로 예측

# soft voting
log_clf = LogisticRegression(solver='lbfgs', random_state=42)
rnd_clf = RandomForestClassifier(n_estimators=100, random_state=42)
svm_clf = SVC(gamma='scale', probability=True, random_state=42)
soft_voting_clf = VotingClassifier(
estimators=[('lr', log_clf), ('rf', rnd_clf), ('svc', svm_clf)],
voting='soft'
)
soft_voting_clf.fit(X_train, y_train)
for clf in (log_clf, rnd_clf, svm_clf, soft_voting_clf):
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print(clf.__class__.__name__, accuracy_score(y_test, y_pred))
"""
LogisticRegression 0.864
RandomForestClassifier 0.896
SVC 0.896
VotingClassifier 0.92
"""- soft voting의 예측 결과 정확도가 더 높은 것을 알 수 있습니다
◆ Bagging
같은 알고리즘으로 여러 개의 분류기를 만들어서 soft voting으로 최종 결정하는 방법입니다.
훈련 데이터 셋으로부터 무작위로 subset을 구성하여 분류기를 각기 다르게 학습시킵니다

- subset은 중복을 허용하여 샘플링을 진행합니다
- 중복 허용한 resampling을 bootstrapping이라고 합니다
- ⇒ bootstrapping + aggregating = bagging
- bagging은 과적합을 방지하는 효과가 있습니다
- bagging은 병렬처리되어 parall(평행)하게 멀티 프로세스를 해도 별 문제가 없습니다.
[ pasting ]
pasting은 bagging과 유사하지만, subset을 만들 때, 중복을 허용하지 않고 샘플링을 진행한다는 점에서 차이가 있습니다.
- bagging은 부트스트래핑(중복 허용) 기반이므로 subset에 다양성을 증가시켜 pasting에 비해 편향이 높습니다. 하지만, 다양성을 증가시킨다는 것은 예측기들의 상관관계를 줄이므로 앙상블의 분산을 감소시켜 안정성이 증가합니다,
- 일반적으로, bagging이 더 나은 모델이 나오는 경우가 많습니다
- 그래도, 교차 검증을 통해 bagging vs pasting 중 더 우수한 방법을 활용하도록 합시다!
[ oob 평가 ]
subset을 만들 때, 어떤 샘플은 여러번 샘플링되고, 어떤 샘플은 전혀 선택되지 않을 수 있습니다. 이 때, 전혀 선택되지 않은 샘플을 oob샘플(out of bag)이라고 합니다.
- 모델을 검증할 때, 별도의 validation set을 만들지 않고 oob 샘플을 사용할 수 있습니다
- 예측기가 훈련되는 동안에는 oob 샘플을 사용하지 않기 때문에 validation set으로 사용가능합니다.
- BaggingClassifier 을 만들 때, oob_score=True로 지정하면, 훈련이 끝난 후에 자동으로 oob평가를 수행합니다.
- oob 샘플에 대한 결정 함수 값은 oob_decision_function_ 변수로 확인할 수 있습니다
- oob_decision_function_ : 각 훈련 샘플의 클래스 확률을 반환합니다.
- oob 샘플에 대한 결정 함수 값은 oob_decision_function_ 변수로 확인할 수 있습니다
bag_clf = BaggingClassifier(DecisionTreeClassifier(),
n_estimators=500,
oob_score=True,
bootstrap=True,
random_state=40)
bag_clf.fit(X_train, y_train)
print('oob_score : ', bag_clf.oob_score_)
print('oob_decision_function : ', bag_clf.oob_decision_function_)
"""
oob_score : 0.8986666666666666
oob_decision_function : [[0.32275132 0.67724868]
[0.34117647 0.65882353]
[1. 0. ]
[0. 1. ]
[0. 1. ]
[0.09497207 0.90502793]
.
.
.
"""
[ bagging 변수 샘플링 ]
bagging은 두 매개변수 max_features와 bootstrap_features로 샘플링을 조절합니다
- 특성 샘플링은 더 다양한 예측기를 만들어 (특정 변수가 많이 샘플링 될 수 있어)편향을 늘리지만, 분산을 낮춥니다.
- 고차원 데이터셋을 다룰 떄에 이 기법이 유용합니다.
[ 변수 중요도 계산 ]
bagging의 결과 값을 확인하기 위해 변수 중요도를 계산합니다
- 랜덤 포레스트는 변수의 상대적 중요도를 계산하기 쉽습니다.
- scikit-learn은 랜덤 포레스트 모형이 가진 모든 트리(예측기)에 걸쳐 평균적으로 불순도를 얼마나 감소시키는 지를 확인하여 변수의 상대적 중요도를 측정합니다
- 이 후, 변수 별 중요도 전체 합이 1이 되도록 정규화를 진행합니다
- feature_importances_ 에 저장되어 있습니다.
- 이 후, 변수 별 중요도 전체 합이 1이 되도록 정규화를 진행합니다
- 결정 트리 기반의 모델은 모두 특성 중요도를 제공합니다
- DecisionTreeClassifier의 특성 중요도는 일부 특성을 완전히 배제시키지만, 무작위성이 증가한 RandomForestClassifier는 거의 모든 특성에 대해 평가할 수 있습니다.
- 랜덤 포레스트의 특성 중요도는 각 결정 트리의 특성 중요도를 모두 계산해서 더한 후, 트리 수로 나눈 값입니다.
import matplotlib as mpl
def plot_digit(data):
image = data.reshape(28, 28)
plt.imshow(image, cmap = mpl.cm.hot,
interpolation="nearest")
plt.axis("off")
plot_digit(rnd_clf.feature_importances_)
cbar = plt.colorbar(ticks=[rnd_clf.feature_importances_.min(), rnd_clf.feature_importances_.max()])
cbar.ax.set_yticklabels(['Not important', 'very important'])
plt.savefig('mnist_feature_importance_plot')
plt.show()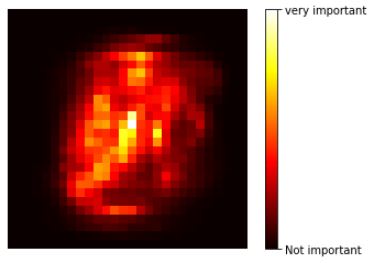
- 중심부로 갈수록 특성 중요도가 높아진다는 것을 알 수 있습니다.
① Random Forest
bagging(or pasting)을 적용한 결정트리의 앙상블로, bagging의 대표적인 알고리즘입니다
- max_samples로 훈련 데이터 셋의 크기를 지정합니다.
- 랜덤 포레스트 알고리즘은 트리의 노드를 분할할 때, 전체 특성 중에서 최적의 특성을 찾는 대신, 무작위로 선택한 특성 후보 중에서 특성을 찾는 방식입니다.
- 무작위성이 더 증가하며, 이 과정에서 트리를 더 다양하게 만들어 편향을 늘리는 대신 분산을 낮추어 전체적으로 더 나은 모델을 만듭니다.
- 아래 코드를 통해, 단일 결정 트리보다 정확도가 높다는 것을 확인하실 수 있습니다.
# Decision Tree (단일 결정 트리)
tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train, y_train)
y_pred_tree = tree_clf.predict(X_test)
# Bagging
bag_clf = BaggingClassifier(DecisionTreeClassifier(),
n_estimators=500,
max_samples=100,
bootstrap=True,
random_state=42)
bag_clf.fit(X_train, y_train)
y_pred_bag = bag_clf.predict(X_test)
print('Decision Tree accuracy : ', accuracy_score(y_test, y_pred_tree))
print('Bagging accuracy : ', accuracy_score(y_test, y_pred_bag))
'''
Decision Tree accuracy : 0.856
Bagging accuracy : 0.904
'''
② Extra Trees
트리를 더욱 다양하게 만들기 위해 최적의 임계값을 찾는 대신 후보특성을 사용해 무작위로 분할한 다음 그중에서 최상의 분할을 선택하는 방식입니다.
- 마찬가지로 편향은 늘어나지만, 분산은 낮춥니다.
- 모든 노드에서 특성마다 최적의 임계값을 찾을 필요가 없기 때문에, 일반적인 랜덤 트리보다 빠릅니다.
◆ Boosting
여러 개의 약한 학습기를 연결하여 순차적으로 학습해 강한 학습기를 만드는 앙상블 방법입니다.
약한 학습기 여러 개를 순차적으로 학습과 예측을 반복하면서 잘못 예측한 데이터에 가중치를 부여하고, 오류를 개선해 나가는 학습 방식입니다.
① Adaboost
이전 모델이 과소적합했던 훈련 샘플의 가중치를 업데이트하면서 순차적으로 학습하는 방식입니다.
- 새로운 예측기는 학습하기 어려운 샘플에 점점 맞춰지도록 훈련됩니다.
- 과적합이 될 위험이 있습니다
- 편향과 분산을 줄일 수 있습니다
[ Adaboost 학습 방식 ]
순차적으로 아래 작업을 반복합니다

- 훈련 데이터셋을 샘플링한 새로운 subset을 생성하고 이를 사용하여 모델을 학습
- 학습시킨 모델을 검증(validation)
- 검증 과정에서 잘못 예측된 데이터를 훈련 데이터셋에 추가하고 새로운 subset을 샘플링 (즉, 오류데이터에 가중치를 부여하여 샘플링될 떄 더 잘 뽑히게 만들고, 새로운 모델의 학습을 진행)
- 모델이 2개 이상 되었으므로 이를 voting하여 하나의 예측값으로 하고 다시 가중치를 계산하여 샘플링이 잘되게 함.
from sklearn.ensemble import AdaBoostClassifier
ada_clf = AdaBoostClassifier(
DecisionTreeClassifier(max_depth=1),
n_estimators=200,
algorithm='SAMME.R',
learning_rate=0.5,
random_state=42
)
ada_clf.fit(X_train, y_train)② Gradient Boosting
앙상블의 이전까지의 오차를 보정하도록 예측기를 순차적으로 추가하는 방식입니다
[ Gradient Boosting 학습 방식 ]
각 step에서 손실함수를 계산하고, 각 과정에서 예측값을 이용해 손실 값의 gradient(미분값)을 계산하여 최적화합니다
- Adaboost와 같이 매 반복마다 샘플의 가중치를 수정하는 것이 아닌, 이전 예측기가 만든 잔여 오차(residual error)에 새로운 예측기를 학습시킵니다.
- 트리가 앙상블에 추가될수록 앙상블 예측이 좋아집니다.
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg1.fit(X,y)
y2 = y - tree_reg1.predict(X) # 첫번째 결정트리에서의 오차
tree_reg2 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg2.fit(X,y2)
y3 = y2 - tree_reg2.predict(X) # 두번째 결정트리에서의 오차
tree_reg3 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg3.fit(X,y3)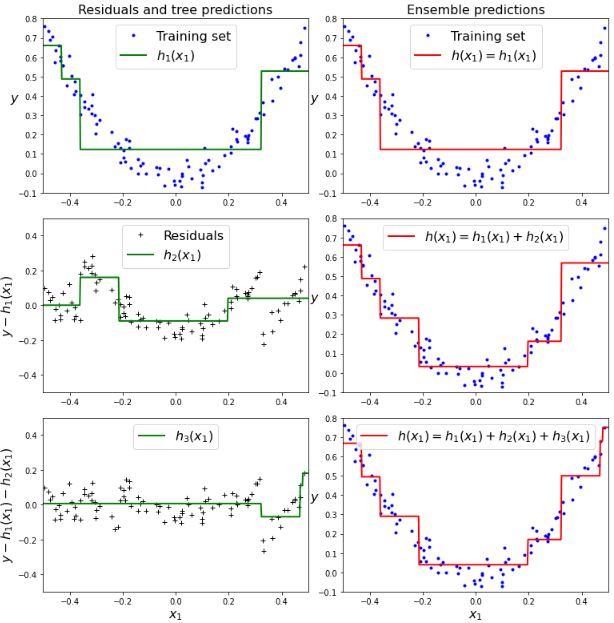
- (좌) 오차의 평균이 0으로 수렴해가는 것을 확인할 수 있습니다.
- (우) 트리가 추가될수록 앙상블 예측이 좋아지는 것을 확인할 수 있습니다.
[ gradient boosting - Early Stopping ]

트리(예측기)가 추가될수록 앙상블 예측이 좋아지지만, 너무 많은 트리가 사용되면 위 그림(우)처럼 과대적합이 발생할 수 있습니다. 그래서 MSE를 사용해 error를 계산해 최소값을 가지는 지점에서 조기 종료를 통해 최적의 예측기 개수를 알 수 있습니다.
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
X_train, X_val, y_train, y_val = train_test_split(X, y, random_state=49)
gbrt = GradientBoostingRegressor(max_depth=2, n_estimators=120, random_state=42)
gbrt.fit(X_train, y_train)
errors = [mean_squared_error(y_val, y_pred)
for y_pred in gbrt.staged_predict(X_val)]
bst_n_estimators = np.argmin(errors) + 1
gbrt_best = GradientBoostingRegressor(max_depth=2, n_estimators=bst_n_estimators, random_state=42)
gbrt_best.fit(X_train, y_train)
min_error = np.min(errors)
print(min_error)
"""
0.002712853325235463
"""
- 어느 정도 유예를 갖는 조기 종료
- error가 최소값을 갖다가 다시 증가하는 경우가 있을 수 있기 때문에, 어느정도의 유예를 설정하여 최적의 결과를 도출합니다.
# 5 epochs동안 에러가 증가하지 않으면 종료
gbrt = GradientBoostingRegressor(max_depth=2, warm_start=True, random_state=42)
min_val_error = float("inf")
error_going_up = 0
for n_estimators in range(1, 120):
gbrt.n_estimators = n_estimators
gbrt.fit(X_train, y_train)
y_pred = gbrt.predict(X_val)
val_error = mean_squared_error(y_val, y_pred)
if val_error < min_val_error:
min_val_error = val_error
error_going_up = 0
else:
error_going_up += 1
if error_going_up == 5:
break # early stopping
print(gbrt.n_estimators)
print("Minimum validation MSE:", min_val_error)
"""
61
Minimum validation MSE: 0.002712853325235463
"""②-1 XGB (Extreme Gradient Boosting)
- 빠른 속도와 확장성, 이식성을 갖추고 있습니다
- 병렬처리가 가능합니다
- decision tree 모형을 만들 때 가지치기 조건을 추가할 수 있습니다.
- 하드웨어에 최적화 가능합니다(gradient 통계값 캐시 메모리 활용)
- 규제를 활용할 수 있습니다(L1, L2, Early stopping)
- sparsity를 인식할 수 있습니다
- Weighted Quantile Sketch 기능으로 최적의 분기점을 찾는데 탁월합니다.
- 자체적 교차 검증 기능이 built-in 되어 있습니다.
②-2 LGB (Light Gradient Boosting)
- LGB은 GOSS(Gradient-based One-Side Sampling)를 메인 기술로 사용하고 있습니다
- GOSS : Information gain을 할 떄, 기울기(가중치)가 작은 개체에 승수 상수를 적용하여 데이터를 중폭시킵니다.
- 속도와 성능 측면에서 XGB보다 뛰어납니다(특히 속도)
- LGB 모형은 Leaf-wise(리프 중심 분할)방식을 활용하기 때문에 깊은 트리를 만들 수 있고, 소요시간 및 메모리를 절약합니다. (확장하기 위해서 max delta loss를 가진 leaf를 선택하게 되는 것)
- 일반 Gradient Boosting모형들은 level-wise(균형트리분할) 방식 (트리를 균형있게 분할)
- 동일한 leaf를 확장할 때, leaf-wise 알고리즘은 level-wise 알고리즘보다 더 많은 loss, 손실을 줄일 수 있습니다.
- (단점)적은 데이터(약 10,000건)에 대해서는 overfitting이 발생하기 쉽습니다
②-3 CatGB (Categorical Gradient Boosting)
범주형 변수들을 처리하는데 중점을 둔 알고리즘입니다.
- 기존 Gradient Boosting 기반 알고리즘들이 가지고있는 target leakage 문제와 범주형 변수 처리문제를 새로운 범주형 변수 처리 방법으로 해결하고자 나온 모형입니다
- 범주형 변수 처리 방법
- Ordering Priciple
- Oblivious Decision Tree(망각 결정 트리) : 트리를 분할할 때, 동일한 분한 기준이 전체 트리 레벨에서 적용되는 범주형 변수 처리 방법
- 균형적인 트리를 만들 수 있고, overfitting을 방지할 수 있습니다
- Feature Combination : 범주형 변수 조합으로 새로운 변수 조합을 생성하는 범주형 변수 처리 방법
- 타겟 누수(Target leakage)는 예측 시점에서 사용할 수 없는 데이터가 데이터 셋에 포함되어 있을 때 발생합니다.
- 범주형 변수 처리 방법
- 기존 LGB는 매번 boosting round에서 범주형 변수를 gradient statistics를 활용해서 변환했기 떄문에 계산 시간과 메모리를 많이 소모했던 것과 비교됨
- 학습 속도 LGB>CatGB
- 예측시간은 CatGB가 가장 빠름
- (단점)데이터 대부분이 수치형일 경우 큰 효과를 내기 어려움
◆ stacking
각 모델을 병렬적으로 추론하고 결과를 취합해서 다시 학습하는 높은 계층의 Meta Model로 새로운 결과값을 얻는 방법

- 개별적인 여러 알고리즘을 서로 결합해 예측 결과를 도출한다는 점이 bagging과 boosting과 유사하지만, stacking은 개별 알고리즘으로 예측한 데이터를 기반으로 Meta Model을 사용해 다시 예측 수행합니다
- 개별 알고리즘의 예측 결과 데이터셋을 최종적인 메타 데이터셋으로 만듭니다
- 별도의 알고리즘으로 최종학습을 수행합니다
- 테스트 데이터 기반으로 메타모델을 사용해 다시 최종 예측을 합니다
- 개별적인 모델들과 최종 메타 모델 두 종류로 나뉩니다
- 최종 메타모델 : 개별 모델들의 예측데이터를 학습데이터로 사용하는 모델
- stacking모델은 일반적으로 성능이 비슷한 모델들을 결합해서 좀 더 나은 성능 향상을 도출하기 위해 사용됩니다
- scikit-learn에서 stacking을 제공하지 않기 때문에 직접 코딩해야 합니다
포스팅 중에 있는 소스 코드는 아래 깃허브 주소에서 보실 수 있습니다(●'◡'●)(●'◡'●)
GitHub - sonzwon/TIL_DL
Contribute to sonzwon/TIL_DL development by creating an account on GitHub.
github.com